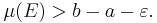Lusin's theorem

In the mathematical field of real analysis, Lusin's theorem (or Luzin's theorem, named for Nikolai Luzin) states that every measurable function is a continuous function on nearly all its domain. In the informal formulation of J. E. Littlewood, "every function is nearly continuous".

Statement

For an interval [a, b], let

f:[a,b]\rightarrow \mathbb{C}

be a measurable function. Then, for every ε > 0, there exists a compact E ⊂ [a, b] such that f restricted to E is continuous and

\mu ( E ) > b - a - \varepsilon.\,

Note that E inherits the subspace topology from [a, b]; continuity of f restricted to E is defined using this topology.

A proof of Lusin's theorem

Since f is measurable, it is bounded on the complement of some open set of arbitrarily small measure. So, redefining f to be 0 on this open set if necessary, we may assume that f is bounded and hence integrable. Since continuous functions are dense in L1([a, b]), there exists a sequence of continuous functions gn tending to f in the L1 norm. Passing to a subsequence if necessary, we may also assume that gn tends to f almost everywhere. By Egorov's theorem, it follows that gn tends to f uniformly off some open set of arbitrarily small measure. Since uniform limits of continuous functions are continuous, the theorem is proved.

References